Pythonを用いて二分探索法を実行します。
■Python
Google Colaboratory(Google Colab),2023年1月20日時点ではPython 3.8.10が用いられる。
Pythonを用いて二分探索法を実行する
では、早速Pythonを用いて二分探索法を実行するコードを書いていきます。
■コード
x = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
# 探索する値を定義
search_value = 5
# 二分探索を実行
low = 0
high = len(x) - 1
while low <= high:
mid = (low + high) // 2
if x[mid] == search_value:
print(f'{search_value}は{mid}番目に見つかりました')
break
elif x[mid] < search_value:
# 中央の値より大きい場合は探索範囲であるlow変数を変更
low = mid + 1
else:
high = mid - 1
# 中央の値より小さい場合は探索範囲であるhigh変数を変更
else:
print(f'{search_value}は見つかりませんでした')まず、今回はxという変数を定義し、その中に角括弧”[ ]”を用いて探索するリストを定義します。リスト内にはカンマ”,”を用い要素(値)を格納します。
格納後、search_valueという変数を定義します。これは探索する値となります。定義した変数内には、探索する要素(値)を格納します。今回は「5」とします。
格納後、lowという変数を定義し、その中に要素(値)として「0」を格納します。highという変数を定義し、その中でlen()を用います。括弧内には引数,パラメータとしてx変数を渡します。これでx変数のオブジェクトの長さ、要素の数が取得されます。取得後、算術演算子”-(マイナス,減算)”を用いて、探索する要素(値)を除くため、「-1」とします。
その後、while文を用います。条件式として、比較演算子”<=”を用いて「low変数がhigh変数以下である」という設定をします。これで指定した条件式がTrue(真)の間、処理を繰り返します。次に、midという変数を定義し、探索する値を探すために中央の値を設定します。今回はlow変数とhigh変数を算術演算子”+(プラス,加算)”を用いて加算します。加算後、スラッシュ2つを用いて、割り算と切り捨てを行います。これで中央の値が設定されます。
そして、中央の値が探索する値と等しい(比較演算子では”==(イコール2つ)”)、またはTrue(真)の場合は、print()で探索する値が見つかったという日本語の文字列が出力されます。出力後、break文でループから抜ける処理となります。等しい場合ではない時はelifを使った複数の条件分岐を設定して、探索する値を絞り込んでいきます。さらにwhile文を用いた処理の繰り返しでも、探索する値が見つからない(False(偽)だった)場合にはelse節でprint()で探索する値が見つからないという日本語の文字列が出力されます。
■実行・検証
では、このセル(コード)を実行してみます。
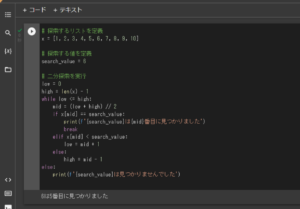
実行してみると、探索する値を二分探索法を用いて探索し出力させることができました。


コメント